「黄金比」・・・

「知っている・聞いたことがある」という方が半数くらいかも知れない。今回「黄金比」を取り上げるにあたり、過去のコラムでも書いてきた「UI/UX雑感」の続編とするかどうか、考えた末に「UI/UX」を外した。

「黄金比」は、デザインの世界に閉じたものではなく、あまりにも神秘的な存在であり魅力的なものだった。前編と後編、２回でその魅力に触れてみたい。

【デザインの黄金比】

The Golden Ratio

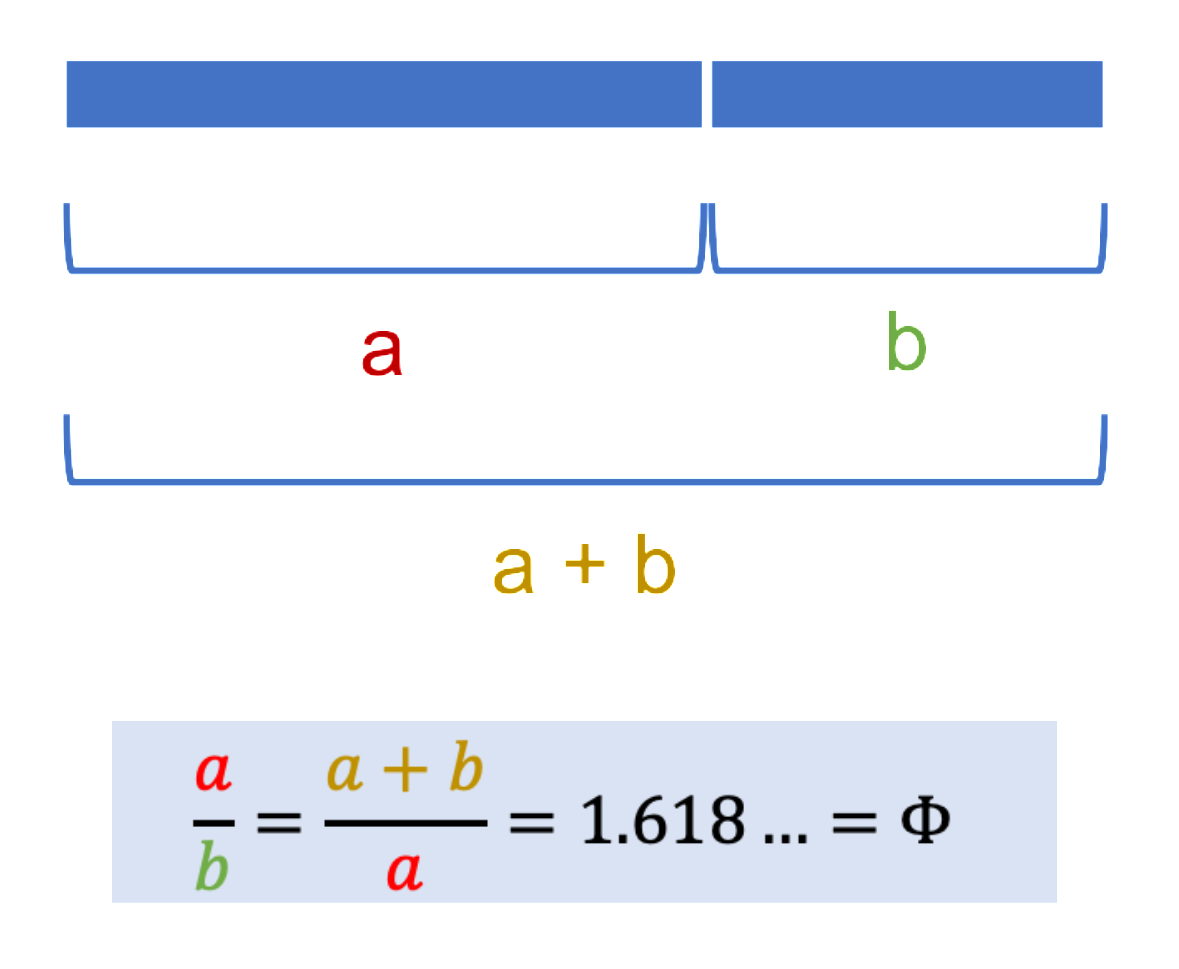
黄金比（Golden Ratio）の「比率」は、「1:(1+√5)/2 ＝1.618… ≒ 5:8」。

一本の線を２つに分割し、短い線に対する長い線の割合が1.618、また、長い線に対して全体の線の割合が1.618となる。
これを黄金比と言い、ギリシャの彫刻家フィデアスの頭文字をとって、Φ（ファイ）で表す。

Φは1.618と小数点３桁で確定するのではなく、ずっと続く無理数である。

プラトンは、「１本の線分をとり、それを等しからざる部分に二分せよ」と言った。
線を二等分したならば、a:b=1:1、a+b:a=2:1で、同じ比率にはならない。しかし、黄金比はこの等式（図内）を成立させる。

プラトンが「線分」で黄金比の問いを投げかけたのは、1.618…が無理数なことを理解していたからであり、幾何学としての表現が可能であるから。

デザインにおいて、黄金比は調和と美しさを与えてくれる。

アテネのパルテノン神殿、エジプトのピラミッド、モナ・リザの顔、パスポート、名刺、Appleのロゴ、ペプシコーラのロゴ、Twitterのロゴなど、様々な建造物やデザインに黄金比は現れる。

また、オードリー・ヘップバーンやアンジェリーナ・ジョリーなど、美しいと言われる顔もそこに黄金比が隠れているとされる。

Apple Logo：黄金比
（ 画像引用：https://creators.view.cafe/122/）

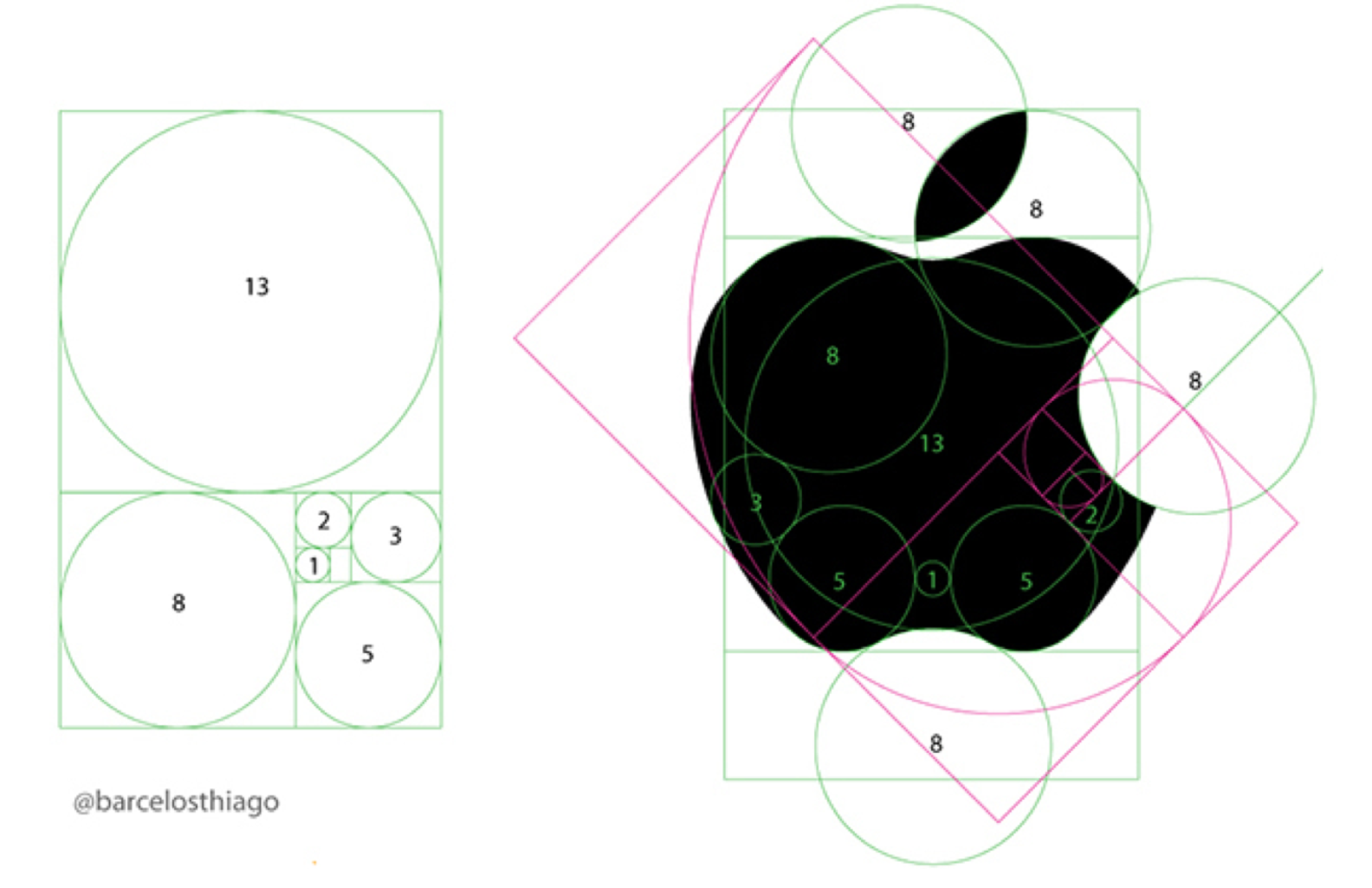
黄金比は1.618と言った。ではAppleのロゴのどこが黄金比なのか？

ここで、「フィボナッチ数列」が登場する。

フィボナッチ数列とは、
1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987…と続く数列であり、法則は前の２つの数を足した数の連続である。

Appleのロゴ内に現れるデザイン上の円の大きさは、全て1,2,3,5,8,13といったフィボナッチ数となっている。

なお、Appleのロゴはロブ・ジャノフがフリーハンドで作ったものであり、黄金比を意識していなかったという話もある。たまたまとしても、人が感ずる美しさの裏には、やはり黄金比があるのではないか。

【フィボナッチ数列】

レオナルド・フィボナッチ
（1170年頃〜1250年頃）

名が残っているレオナルド・フィボナッチは、中世イタリアの数学者。

彼の最も有名な処女作「算盤の書」の冒頭では、このように書かれている。

　

「九つのインド数字は、９、８、７、６、５、４、３、２、１。
この九つと記号０によって・・・どんな数も以下に明らかにするとおり書き表せる」

　

これは、当時のローマ数字（Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅶ、Ⅷ、Ⅸ、Ⅹ、50はL、100はC）よりインド数字が単純で効率的であり、いちばん優れていると考えたため。フィボナッチの考えが正しかったことは、0、1〜９の利用が現在の標準であることが証左だ。

では、フィボナッチ数列と黄金比の関係とは何か。

　

　

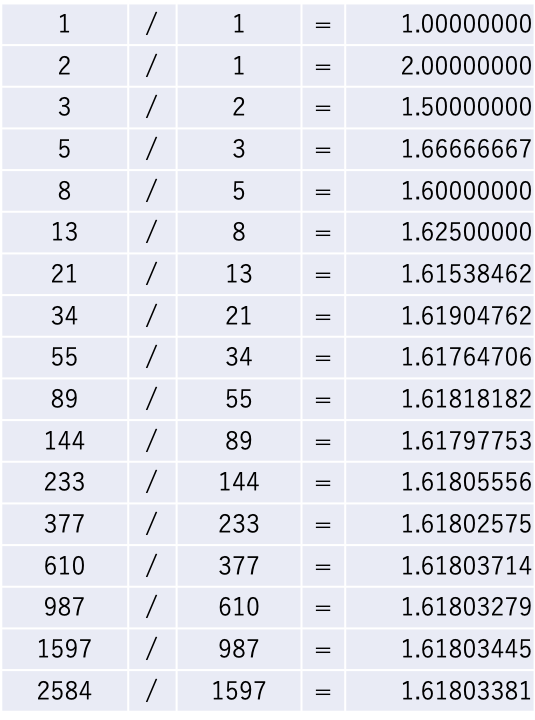
フィボナッチ数列での連続する２つの比をみてみよう。

1/1=1、2/1=2、3/2=1.5、5/3=1.66666・・・表にしてみた。

89/55でも現れるが、233/144以降の商は1.618…。

n番目のフィボナッチ数をF_nとし、その次をF_(n+1)とすれば、比F_(n+1)/F_n はnが大きくなるにつれΦに近づく。

この性質はドイツの天文学者ヨハネス・ケプラーが発見したと言われている。

もともとフィボナッチ数列は、先ほどの書「算盤の書」において、「ウサギの出生率に関する数学的解法」などの解法であった。

ウサギの出生率

ある男がウサギのつがいを壁で囲まれた場所に放した。 どのつがいも毎月新しいつがいを生み、生まれたつがいは次の月からつがいを生むとすれば、１年間に何対のウサギが生まれるだろうか？

図のウサギのイラストで、大人ウサギの対の数は、1,1,2,3,5、子供ウサギの対の数は、0,1,1,2,3と、まさにフィボナッチ数列となる。

フィボナッチ数列は前２つの数の和として、急速に大きな数となっていく。

5ヶ月目のウサギの対の数が８、2年（24ヶ月）後には75025、3年（36ヶ月）後には24157817になる。

ウサギにしてもネズミにしても、死なずに生み続けていたなら、この世界は大変なことになる。

【白銀比】

前編の最後に、黄金比とともに知られている「白銀比」を紹介する。

白銀比の比率は1:1.414≒1:√2　、日本ではよく使われており大和比という別名もある。

　

法隆寺、見返り美人図、スカイツリー、ドラえもん、キティちゃん、などに応用されている。もっとも身近なのはコピー用紙。
A1からB3まで全て白銀比の長方形であり、長方形の長辺で2等分すると、相似の長方形が現れる。A3の2等分ならA4、A4の2等分ならA5になる。

今回、興味があった黄金比について書こうと思い立ったが、参考とする文献がなかなか読み進まなかったり、またネット上での黄金比の記事も実に多く、情報によっては否定的なものもあって、時間を要してしまった。

黄金比とフィボナッチ数列、前編はデザインと数学的な部分に言及したが、「神秘的」な面に触れるのは後編としたい。

参考・参照文献
「黄金比はすべてを美しくするか？」（マリオ・リヴィオ、斉藤隆央〔訳〕）ハヤカワ文庫
「黄金比 自然と芸術にひそむもっとも不思議な数の話」（スコット・オルセン、藤田優里子〔訳〕）創元社
「波紋と螺旋とフィボナッチ」（近藤滋）秀潤社

参考・参照記事
http://amanafarm.naganoblog.jp/e2009912.html

文責：永井一美